自己紹介（井沢開理）

経　歴

・1961　防衛大学校卒業
　　　 　 陸上自衛隊入隊
・1990　自衛隊退職
　　　　 東京工学院専門学校コンピュータ教員
・1997 　同校退職
　　　　　㈱日本ネットワーク千葉設立（しばらく経営するも、その後息子に経営を譲る）

・2004　【応用ゲーム理論の結論】朱鳥社　
　　　　　全国図書館流通のストックブックに指定される（4-434-0489-0/2004.9)　故に国会図書館で　　　　　半永久的に保存され、そして有名大学の図書館で購入されている。
　2011　【ゲーム理論から見た　尖閣諸島・沖縄基地問題】東京図書出版
・以後、講演活動等

※　学生時代レスリング部に所属していたため、体力には自信があった。
　　自衛隊のトップは、「智信仁勇厳」が必須だが、中堅以下には、体力及び強固な
　　精神力が必要である。
　　自衛隊体育学校（幹部格闘課程）で体力および精神に磨きをかけ、自衛隊式格闘技指導員、
　　銃剣道五段の資格確保。しかし自分の不注意により腰を痛め朝、顔を洗う程度の前屈さえ出来なく　　なった。これではもう第一線の隊員として「使い物」にならない。
　 　そこで上司の計らいにより、不本意ながら自衛隊業務学校（幹部運用解析課程）で
　　一年間、数学（微分積分、確率統計、行列等）を中心に、戦闘理論、射撃爆撃理論、
　　ゲーム理論等をみっちり勉強した。

　　なお私は、勉強ほど嫌いなものはなかった。
　　しかし自分の得意分野「体力」を失った今、ただ妻子を食わせるためには「勉強しかない」と自覚し　　、必死になって勉学に励んだ。
　　そこで初めて「勉強の面白さ」を知った。勉強が面白くて仕方なかった（もう少し早く、知っておけば良かった…）。

　　同課程修了後、同課程教官に就任。
　　以後、主として教育・研究・コンピュータ関連業務に従事。
　　業務学校教官時代、教範として「確率論」「射撃爆撃理論」を著す。
　　そして戦闘理論では有名なランチェスターの戦闘理論式

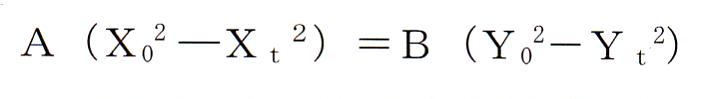
　に代わる新戦闘王理論式として

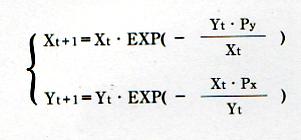
を考案する。　
参考資料

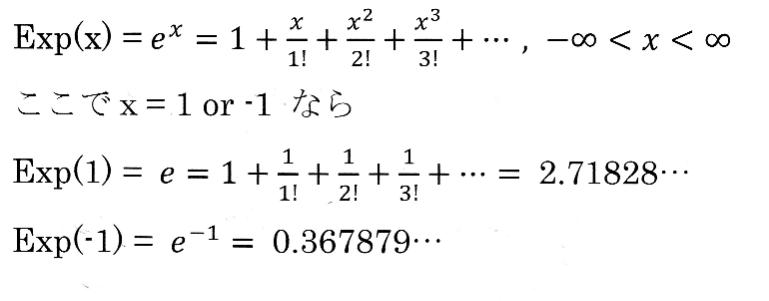
　この当時「関数計算機」がまだなく、一般技術者は数表を使い、ｅ・Log等の計算をしていた。
　ただしここに、世界で唯一ヒューレット・パッカード社の「関数計算機モデル67」が存在していた。
　この計算機は、単に関数計算だけでなく、プログラムまで組める計算機であった。
　そして価格は、16万円であった。それは当時、私の給料の２倍以上の価格であった。
　私は、無理して上記計算機を買って、戦闘理論式のプログラムを組んで諸計算を実施した。
　ただし、誰も計算機すら持たない時代に、私のこの戦闘理論式は、自衛隊内で認められることはなかった。 プログラム付き計算機でなければ、上記計算式の連続計算はできない。（時代に早すぎる先駆者は、その時代では認められないものらしい）。
　ただし、現在「Excel」で上記計算式を簡単に組むことが出来る。
　その一例をこのページの末尾に添付するので、興味ある人は参考にされたい。

　そこで、ここに社会に役立つ「算数の問題」を次に提示する。簡単で面白い問題と思うので、ぜひ挑戦して欲しい。

平均値の問題　（想定とケンカすることを禁ず）

　N国は、祖国防衛のためヤマト・ムサシという２大戦車を有する平和を愛する国家である。
　勿論戦車は、コンピュータで十分管理されており、管理表の一例は次のとおりである。

  走行km 累計故障回数 平均故障距離（km）
ヤマト 1,200 6 200
ムサシ 600 2 300
合計 1800 8 X

　S国からの執拗な領土要求を拒否したN国は、遂にS国からの侵略を受けることになった。
　この不当なS国からの侵略を阻止すべくヤマト・ムサシは国民の歓呼の声に送られて、1200km離れた隘路を通過して今戦場へ向った。
　ここに堅実な人柄で知られる戦車大隊幕僚・A少佐は、過去の実績から、戦車ヤマトの予想故障回数は　□回、戦車ムサシの予想故障回数は □回　
合計 　□回と見積もった。
　一方中央にあって兵站幕僚B中佐は、大所高所の立場にある者として一台々々計算するようなことはしない。管理表にあるXを使い、1200×２／X＝　□回と計算し、関係部署との調整に着手した。
　なおこれは当然の結果であってあえて書く必要はないが、両幕僚の見積は、
　　　　　　　　　　　　　　　　　　　　完全に一致していた(ホントかな？）。

　この問題の文章・数字はナンセンスだが、「平均値に関し重要な問題」を含んでいる。
　多分どう計算しても「完全に一致」しない人が大部分でしょう。
　答えは、このページの末尾にあります。

 

拙著について

６桁キューブについて

　左図は、私が76歳の時、月刊誌「シルバー人材センター」に投稿したものである。
　昭和55年頃、3桁のルービック・キューブの大ブームがあった。簡単そうに見えるが、少し動かしただけで画面が（上下左右前後）に変化するため、誰も仲々揃えられず、カンニングペーパーが発売されるようになって、出来る人が少し出た程度であった。
　私は本来こういうことが大好きだったので、その頃かなり苦労してようやく出来るようになった。
　その30余年後、孫のために何かないか探していた時、「6桁のキューブ」を発見して驚いた。まさか6桁のキューブが開発されるとは思わなかったし、同時に「売れるはずがない」と思った。　多分メーカーは、自社の技術力を誇示するため採算を度外視して販売したものであろう。
　それはさておき、同時に76歳という年齢を忘れ「やってやろうじゃないか！」という闘志も内から湧いてきた。
　やってみると、3桁キューブにない手法の連続であった。そして3桁キューブの何倍かの努力で、ようやく6桁キューブ攻略に成功した。
　6桁キューブ攻略して何になるか？
　単なる自己満足にすぎない。
　しかし年を取っても、「自分の得意なことは衰えない」［古い童謡：村の渡しの船頭さんは、今年60のおじいさん。年は取ってもお舟を漕ぐときは、元気一杯櫓（ろ）が軋（きし）む。：この時代日本人の平均寿命は60未満。渡し舟が存在していた頃の童謡］この発見は大きかった。
　年を取って体力・記憶力は大幅に減少した。しかし「自分の得意なことは衰えない」、これが大きな自信になり、以後ゲーム理論研究に熱（力）が入るようになった。
　皆様方も、年を取られても自分の得意であった趣味・特技（囲碁・将棋、盆栽、料理、過去自分が得意であった勉強等）を生かされては如何でしょうか。
　殆ど実力が落ちていないことに、驚かれるでしょう。

 

　先に年配の人に呼び掛けたが、今度は若い人に呼び掛けたい。

　夏休み等暇なときに、スマホだけでなく「頭の体操」として「3桁キューブ」に挑戦されては如何でしょうか。

　「頭の体操」としてはかなり高度の部類に入ると思われます。まず攻略するまでに1 ｹ 月は、覚悟する必要があるでしょう。
　そして揃えるのに「上から順に揃える方法」と「４隅から揃える方法」があります。「４隅から揃える方法」の方が、「多桁キューブ」に挑戦するためにいいでしょう。
　ただしここで「最初の４隅を揃える」ことは誰にでも出来るが「次（下）の４隅を揃える」ことが大変難しく、大多数の人がここで挫折するでしょう（自力で出来る人は、大学生で１％以下と見ています）。
　簡単には揃えられない。そこには「頭の体操」+「忍耐力」が必要です。「全４隅を自力で揃えられた人」ならば以後、難関もありますが、自力で揃えられるでしょう。
　そこから先は、余暇の利用の範囲内で、４桁、５桁、６桁の「キューブ」に挑戦するのもよいでしょう。ただし、あまり熱中しない方が、いいと思います。

平均値の問題　（解答）

ここで考えられる平均値は、トータルの平均値　1800／８＝225㎞
あるいは、平均値の平均値　（300+200）／２=250㎞　位のものだろう。
いずれも「完全に一致」しない。
そこで平均には、「相加平均」「相乗平均」「調和平均」の３つがあります。
今個々の値をｍ1、ｍ2、ｍ3　とし、この３つの平均をｍとした場合、
相加平均は
　　　　ｍ = (m1 + m2 +m3)／3
で計算が簡単で判りやすく、一番多く使われている。
相乗平均は
　　　　ｍ = ∛（m1×m2×m3)　（ルート３）
であり、昔はその計算が困難であったが、現在は関数計算器・エクセルで簡単に計算ができる。
　使用方面は、ロケット全体の安全性は、各部品の相乗平均でなければならないと言われている。
調和平均は、
　　　ｍ = 3／（1／m1 + 1／m2 +1／m3)
で各平均値の調和を考える場合、この調和平均が良いとされる。
　適用される場面は、生徒個人の各学科の総合評価は、調和平均値が望ましいとされるが、それほどの差もないので、相加平均が用いられている。ただし、相加平均と調和平均では、1位2位が入れ替わることも、受験では合否が逆転することもありうる。
さてこの問題に限定すれば、
相加平均値は、
　　　ｍ=(300+200)／2＝250㎞
相乗平均は
　　　ｍ=√（300×200）=√60000≒245㎞
調和平均は
　　　ｍ＝2／（1／300　+　1／200）=240㎞
故にこの調和平均値240を用いれば、
　　　1200×２／240=10回で完全に一致する。
なおパソコンでデータを管理する場合、プログラムを組めば（Exselではもっと簡単に）、済むことであり、一般の人は何も考えず、データー入力すれば良いのであり、統計上広く「調和平均値を使用すべきである」「相加平均だけが万能でない」
これが教訓である。

 

戦闘理論式の計算一例

次は、前に記したように井沢開理が開発した「戦闘理論式」を「Excel」で計算した一例である。

ここで例として、青軍兵士13０名、赤軍兵士100名が小銃を持って対峙したとする。
ただし、青軍兵士の小銃の命中率は0.10、赤軍兵士の小銃命中率は0.13とする。
　この想定の下では、「一見ほぼ同格」のように見えるが…。

　　ただし、「どちらが、どの程度強いのか」、専門家でも頭を悩ますところである。
　白紙的に「どちらが、どの程度強いのか？」それを判断するのが、この「戦闘理論式」です。

　そこで、感情も持たず恐怖心もない、器械的にただ射撃するだけのロボットの兵士を横一線に並んで、勝負が付くまで射撃させるのが、この「戦闘理論式」です。

注：次は、上記計算式で計算した戦闘経過の一例である。である。

　

結果、圧倒的に青軍が強い。発射数（使用弾数）に大きな差が出るからである。

　この計算結果は、一般の人には予想外の結果であろう。

　「両軍の使用弾数も計算できる」のが、この戦闘理論式の特性である。

　この戦闘理論式は、多くの応用法がある。例えば、両軍の発射速度を同等としたが、赤軍兵士の小銃発射速度を上げれば、結果は逆転する（その使用法は、略する）。
　この基本計算式に、発射速度・弾丸威力・陣形等を組入れた応用戦闘理論式もできる。興味ある人は、その応用戦闘式を作り、プログラムを組んで見れば如何でしょうか？
　私は、この戦闘式について、その当時最新式のプログラム付き関数計算機を持ち、種々応用法も考えたが、時代に先過ぎて自衛隊内で、この戦闘式が認められなかったことは残念に思う。

 

夢の夢

　 ある朝、何か衝撃を受けて、はっと目が覚めた。もう自分は長くない。
　自分は、元自衛官、余命いくばくもない。国家国民のために、何かお役に立つことはないかと考えたとき、自分にはゲーム理論しかない、ゲーム理論で「国家国民のために貢献したい」という衝撃に駆られた。
　ただし、「日本の平和」だけでない、「世界の平和」を考えるのが、「新ゲーム理論」である。
　日本には「反日家」が多くいる。彼らは、日本が悪であり、悪である日本を倒すことが、「彼らの正義」であった。
　1960～70代、「連合赤軍」「東アジア反日武装戦線」と名乗る等、「真正面からの反日が正義」、それが通じる時代であり、数々のテロも起こし、その「テロの目的」を達することができても、「本来の大目標」は達成できなかった。その時の「反日過激派」は、その時の行動を「誤りであったと考える人」も、今なお「反日が正義」と考える人もいるようである。
　もう「真正面からの反日が正義」が通じる時代でない。
　しかし「隠れ反日の正義の言動」の方が、もっと強力で深刻である。

日本の危機を訴える有識者も多くいる。「日本を反日勢力から守りたい」と考えている人も多く出てきた。我こそはその先駆者ならんと欲し、天の声を聞きながら、このＨＰの作成に勤しんでいる。